Рассматривается задача минимизации интеграла 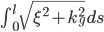 для гладких кривых на поверхности сферы с фиксированными граничными точками, и заданными направлениями в них. Здесь длина кривой
для гладких кривых на поверхности сферы с фиксированными граничными точками, и заданными направлениями в них. Здесь длина кривой 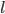 является свободной,
является свободной, 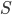 обозначает сферическую длину дуги, и
обозначает сферическую длину дуги, и 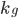 - геодезическую кривизну сферы. Эта задача является естественным продолжением модели Петито [1], Ситти и Сарти [2], учитывающим сферическую природу сетчатки. В докладе будут получены уравнения для геодезических кривых на поверхности сферы, и оценено первое время возврата - минимальное положительное значение параметра вдоль геодезической, при котором возникает точка возврата. Исследуемые кривые являются проекциями субримановых геодезических в левоинвариантной субримановой задаче на группе
- геодезическую кривизну сферы. Эта задача является естественным продолжением модели Петито [1], Ситти и Сарти [2], учитывающим сферическую природу сетчатки. В докладе будут получены уравнения для геодезических кривых на поверхности сферы, и оценено первое время возврата - минимальное положительное значение параметра вдоль геодезической, при котором возникает точка возврата. Исследуемые кривые являются проекциями субримановых геодезических в левоинвариантной субримановой задаче на группе 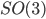 на поверхность единичной сферы. Мы обобщаем результаты Боскаина и Росси [3] на общий случай
на поверхность единичной сферы. Мы обобщаем результаты Боскаина и Росси [3] на общий случай 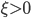 .
.
[1] J.Petitot, The neurogeometry of pinwheels as a sub-Riemannian contact structure, J. Physiology - Paris, 97 (2003), 265—309.
[2] G. Citti and A. Sarti, A cortical based model of perceptual completion in the roto-translation space, J. Math. Imaging Vis., 24 (2006), 307-326.
[3] U. Boscain, F. Rossi, Invariant Carnot-Caratheodory metrics on 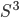 ,
, 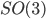 ,
, 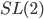 and Lens Spaces, SIAM, Journal on Control and Optimization, Vol 47 (2008), 1851-1878.
and Lens Spaces, SIAM, Journal on Control and Optimization, Vol 47 (2008), 1851-1878.

