Title: On Positive Orthant Controllability of Bilinear Systems in Small Codimensions
Authors: Yu. L. Sachkov
Journal title: SIAM Journ. Control and Optimization
Year: 1997
Volume: 35
Pages: 29—35
Abstract:
For the bilinear control system of the form 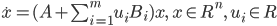 , with
, with 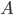 essentially nonnegative and
essentially nonnegative and 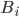 constant diagonal matrices, the following global controllability question is studied: when can any two points in
constant diagonal matrices, the following global controllability question is studied: when can any two points in 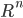 with positive coordinates be connected by a trajectory of this system? The answers for
with positive coordinates be connected by a trajectory of this system? The answers for 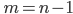 and
and 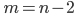 for any
for any  are given; some necessary conditions for other cases are proven.
are given; some necessary conditions for other cases are proven.

