Title: Symplectic geometry and necessary conditions for optimality
Authors: A.A. Agrachev, R.V. Gamkrelidze
Journal title: Mathematics of the USSR-Sbornik
Year: 1992
Issue: 1
Volume: 182
Pages: 29-45
Citation:
A. A. Agrachev, R. V. Gamkrelidze, “Symplectic geometry and conditions necessary conditions for optimality”, Mathematics of the USSR-Sbornik, 1992, 72:1, 29–45
Abstract:
With the help of a sympletic technique the concept of a field of extremals in the classical calculus of variations is generalized to optimal control problems. This enables usto get new optimality conditions that are equally suitable for regular, bang-bang, and singular extremals. Special attention is given to systems of the form 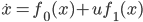 with a scalar control. New pointwise conditions for optimality and sufficient conditions for local controllability are obtained as a consequence of the general theory.
with a scalar control. New pointwise conditions for optimality and sufficient conditions for local controllability are obtained as a consequence of the general theory.
File:
Download
MathNet (ENG):
http://mi.mathnet.ru/eng/msb1273

