Title: On the completeness of sparse subsequences of systems of functions of the form 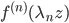
Authors: A. Yu. Popov
Journal title: Izvestiya: Mathematics
Year: 2004
Issue: 5
Volume: 68
Pages: 1025–1049
Citation:
A. Yu. Popov, “On the completeness of sparse subsequences of systems of functions of the form 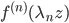 ”, Izvestiya: Mathematics, 2004, 68:5, 1025–1049
”, Izvestiya: Mathematics, 2004, 68:5, 1025–1049
Abstract:
We obtain some new results on the completeness of systems of functions 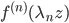 in the space of entire functions with the topology of uniform convergence on an arbitrary compact set in
in the space of entire functions with the topology of uniform convergence on an arbitrary compact set in  " />. In the presence of lacunae in the Taylor expansion of the function
" />. In the presence of lacunae in the Taylor expansion of the function 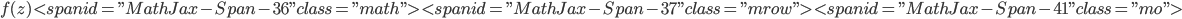 " />, we prove the existence of bases consisting of subsystems of this form.
" />, we prove the existence of bases consisting of subsystems of this form.
MathNet (ENG):
http://mi.mathnet.ru/eng/izv507

